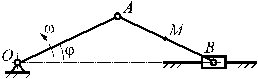|
Problem S1¢2007 (4 points) |
|
|
|
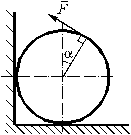
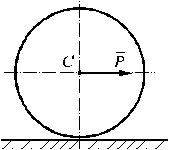
A homogeneous
cylinder with weight G and radius R lay on a rough
horizontal floor and adjoins to a rough vertical wall. What conditions must
be satisfied by the force F enclosed to a
point A of the cylinder to keep it in equilibrium. The
coefficient of friction between the cylinder and the floor is f. The
coefficient of friction between the cylinder and the wall is f too. |
|
Problem S2¢2007 (6 points) |
|
|
|
Cube 1 of weight G1 and edge
length a is put on homogeneous cores 2
and 3 hinged together at C, as shown in
figure.
Rods
each of weight G2 stand on a smooth horizontal
floor. AC = č┼ = ┬č = CD =
= └┬ = l. The system is
kept in equilibrium with the help of spring KL connecting the
middle of pieces AC and ┬č. Determine the force of the
spring tension. |
|
Problem K1¢2007 (6 points) |
|
|
|
There is slider
crank mechanism with OA = AB. Crank OA rotates with angular velocity w. Its position determined by a angle j. Find the size
and a direction of angular acceleration of crank OA, when vectors of speed and acceleration of the center
point M of the connecting rod AB of the slider crank
mechanism are mutually perpendicular. |
|
Problem
K2¢2007 (8 points) |
|
|
|
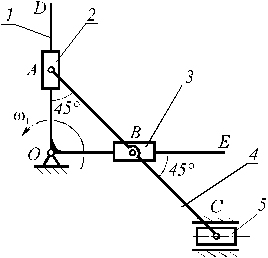
Crank 1 rotates with angular velocity w1. Point B
is the center of the connecting rod AC. OA = l
(Fig.). Determine the velocities and accelerations of the sliders 2 and 3 in
relation to a crank for this position. |
Problem D1¢2007 (5 points) |
|
|
|
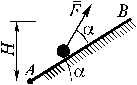
Initially a
particle of mass m = 1 kg is in position A; its velocity is v0 = 10 m/sec and it is directed to
the point B along an inclined plane. Force F changes in accordance with the law F = 20 t . Neglecting
friction, determine rising height H of the particle through t = 2 sec, if a = 30░. |
|
Problem
D2¢2007 (6 points) |
|
|
|
The wheel presents a homogeneous disk with mass m and radius r. The axisÆs C acceleration is connected to the velocity by dependence |
|
Problem
D3¢2007 (7 points) |
|
|
|
The load 1 with mass m1 = m
is on the rough surface inclined at angle a = 45░
to the horizontal (coefficient of friction f = 0,25). Unstretched
cord passes over the pulley 2 mass m2 = m. The pulley 2 is homogeneous circular cylinder. Other end of
the cord is wound on a drum and makes the wheel 3 roll without sliding on a
horizontal surface. There radiuses are Determine the
velocity of the load 1 to the time when it will pass on the inclined plane distance s,
if cord is at the angle b = 30░ to the
horizontal this time. Initially the system was in equilibrium. |
|
Problem
D4¢2007 (8 points) |
|
|
|
Loads 2 and 3 with m2 = 2m, m3 = m
connected to a rod 1 of length l and mass m1 = m. Inextensible
string passing over the pulley 4 of the mass m4 = 2m. String connects centres of gravity
of the rod 1 and wheel 5 with radius r. The wheel rolls without sliding on the inclined plane at angle a = 30░
to the horizontal. The wheels 4 and 5 are homogeneous cylinders. Initially the system was in equilibrium and objects 1
and 5 have equal angular acceleration. At that time cos φ = 0,8. Determine mass of the wheel 5. |