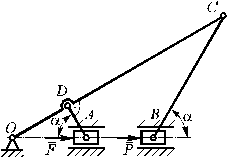Problem S1–2008 (10 points)

The inverse mechanism is located in a horizontal plane. Sliders A and B can move along an axis which are taking place through point O.

It is need to prove, that in the position represented in figure (AD ^ OC, and corners, which rods AD and BC make with axis OB, are identical) the mechanism will be in equilibrium at condition .

Problem S2–2008 (8 points)

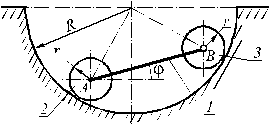
The uniform rod 1 with one of its ends is fixed with disk 2 and the other end is hinged at B with a disk 3. Disk’s radiuses are identical and equal r, and their weights are neglecting. Disks rest on the surface having the form of a semicircle with radius R = 5r. Coefficient of sliding friction between disks and a surface is f. Coefficient of rolling friction between disk 3 and the same surface is δ. Rod length is . Determine maximum value of the angle j between a rod 1 and a horizontal plane when the rod is in equilibrium.

Problem K1–2008 (10 points)

In the planar mechanism crank OA rotates with constant angular velocity ω. OA = BC = = CD = CE =DF = l, . Determine velocity and acceleration of point B for mechanism position when , , a = β = 30°.

Problem K2–2008 (10 points)

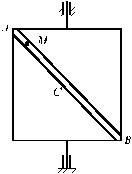
The square plate has uniformly accelerated rotation around a vertical axis. Its initial angular velocity is distinct from zero. Point M moves on diagonal AB of a plate so, that the absolute acceleration vector all the movement time lays in a plate’s plane. During the initial time point M is in position A.

Prove that in a considered case point M will never be lowered below mid-point C of a plate’s diagonal.

Problem D1–2008 (7 points)

Maximum horizontal range of a stone thrown from the immovable catapult is s.

Find the maximum possible horizontal range of the stone thrown from the very catapult but fixed on the platform the mass of which together with the catapult is n times heavier than the stone mass. The platform is on the horizontal plane. At the start time it is motionless. Any resistance can be neglected.

Problem D2–2008 (7 points)

The uniform L-shaped rod with equal cross-sections AB = l and BC = 2l is located in a vertical plane. Rod BC is horizontal.

Point O is attachment place of hinge to the rod BC. Determine distance OB when the rod has maximum angular acceleration.

Problem D3–2008 (8 points)

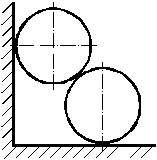
Two identical homogeneous smooth cylinders with radius R are leant against a vertical wall.

The bottom cylinder displaced to the right on a horizontal plane. The top cylinder began to fall on a vertical. The system has come to motion.

Find final velocity of the bottom cylinder.

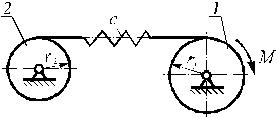
Problem D4–2008 (10 points)

The pulley 1 of weight m₁ and radius r₁ is set in rotation by constant torque of moment M. From pulley 1 through a deformable cable motion is transferred to the pulley 2 of weight m₂ and radius r₂. In this case a cable it is possible replace with a spring which force of a tension is directly proportional to deformation of a rectilinear part of a cable, the proportionality coefficient is equal c.

Determine the law of angular velocity of the pulley 1. Initially the system was in equilibrium.

Both pulleys are assumed to be homogeneous cylinders. Neglect deformations of curvilinear parts of a cable and a friction.